As an example, we can examine the European roulette model (roulette with one zero). Since this roulette has 37 cells with equal odds of hitting, it is clear that this is a final model of field probability 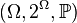 , where
, where 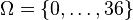 ,
, 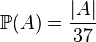 for all
for all  . We’ll call the bet S a three (A,r,ξ), where A for a certain random event|event
. We’ll call the bet S a three (A,r,ξ), where A for a certain random event|event  , and
, and  = random size. The event A naturally leads to a winning event, r to the size of the bet (in dollars, for example), ξ to the bet rule, and the mathematical expectation M[ξ] relates to the bet profitability.
= random size. The event A naturally leads to a winning event, r to the size of the bet (in dollars, for example), ξ to the bet rule, and the mathematical expectation M[ξ] relates to the bet profitability.
The rules of European roulette have 10 types of bets. First we can examine the ‘Straight Up’ bet. It’s clear that in this case,  , where
, where 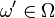 , and ξ is determined by this law
, and ξ is determined by this law
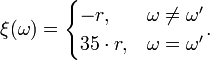
The bet’s probability is equal to
![M[\xi] = \frac{1}{37} \sum_{\omega \in \Omega} \xi(\omega) = \frac{1}{37} \left(\xi(\omega^\prime) + \sum_{\omega \ne \omega^\prime} \xi(\omega)\right) = \frac{1}{37} \left(35 \cdot r - 36 \cdot r \right) = -\frac{r}{37} \approx -0.027r.](https://upload.wikimedia.org/math/a/1/c/a1c4a05105447575136f448fd8860fa7.png)
Without details, for a bet, red or black, the rule is determined as
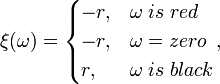
and the profitability ![M[\xi] = \frac{1}{37}(18 \cdot r - 18 \cdot r - r) = -\frac{r}{37}](https://upload.wikimedia.org/math/f/5/a/f5a95373f6ccb30fc39795fcbadc5bf0.png) . For similar reasons it is simple to see that the profitability if also equal for all remaining types of bets.
. For similar reasons it is simple to see that the profitability if also equal for all remaining types of bets. 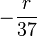 .
.
In reality this means that, the more bets a player makes, the more he is going to lose independent of the strategies (combinations of bet types or size of bets) that he employs:
![\sum_{n = 1}^{\infty}M[\xi_n] = -\frac{1}{37}\sum_{n = 1}^{\infty}r_n = -\infty.](https://upload.wikimedia.org/math/9/6/f/96fba465aeb29fb7086f9bf398e7a823.png)
Here, the profit margin for the roulette owner is equal to approximately 2.7%. Nevethless, several roulette strategy systems have been developed despite the losing odds.
It’s worth noting that the odds for the player in American roulette are even worse, as the bet profitability is 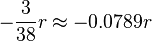 , and the rest are
, and the rest are 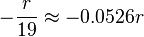 .
.



